Material taught, literature references, homework
Books mentioned are accessible via the literature page.
From home you need to connect with vpn, except for the book by Hollas which is available here.
Numbers given are page numbers.
- 4/10/2024: What is and what is not discussed as Spectroscopy. Quantities involved. Appearance of a spectrum. Basic equations and spectral regions. Blackbody radiation, Einstein coefficients.
- Hollas: xxi-xxv, 27-39, 41-43
Bernath (2nd Ed.): 3-11
McHale: 48-51
Softley: 1-6
Brown: 1-5, 15-17
- 11/10/2024: Einstein coefficients. Line shapes, broadening effects: Natural, Doppler, pressure, etc.
- Hollas: 27-39, 1-8
Bernath: 7-11, 21-34
McHale: 48-51, 153-170
Softley (en): 17-18
Brown (en): 14-17
- Homework
- Problem 1: The double D line of sodium has an average wavelength of 589.29 nm. Write the frequency, the wavenumber, the energy (in J and eV) of its photon. In which spectral region does it belong?
- 18/10/2024: Atomic spectroscopy: Hydrogen-like atoms, wave functions, spin-orbit coupling, fine structure, hyperfine structure, quantum defect theory for spectra of alkali metals.
- Hollas: 34-39, 1-12
Bernath: 109-124, 137-141
Softley: 8-25, 29-35
Sobelman: 3-15, 34-37, 156-162
- Homework
- Problem 2: At what wavenumber dows a black body with a temperature of 37 °C emit its most intense radiation? What part of the electromagnetic spectrum does it fall under?
- Problem 3: How many electrons does 108Ag46+ possess?
- Problem 4: At what wavenumber and wavelength is the 4th Balmer line observed?
- 25/10/2024: Atomic spectroscopy: wave functions, Einstein coefficients and transition dipole moments. Demonstration of UV-vis. spectrophotometer operation and components. Range of visible spectrum. Flame spectroscopy with a Bunsen burner.
- Spectra of H, O, He, Ne, Ar, Na, Li, sun
- 4/11/2024: Rotational spectroscopy: energy levels, angular momentum, moments of inertia of molecules, calculating moments of inertia, types of tops. Diatomic and linear molecules: hamiltonian operator, quantum numbers, energy eigenvalues, wave functions, degeneracy, selection rules, population distributions, peak positions, form of spectra, isotope effect.
-
- Brown: 21-26
Hollas: 103-111
Bernath: 169-177
McHale: 209-212
Carrington: 146-152
Levine: 165-168
- Homework
- Problem 5: Using data from CRC Handbook of Chemistry and Physics (9- 15-41) caclulate the moments of inertia for the moelcules HBr, C2H2, HCCD and their rotational spectroscopic constants (in cm-1). Use the masses of the most abundant isotopes when not specified.
- 8/11/2024: Rotational spectroscopy of non-linear molecules: Hamiltonian operator, quantum numbers, energy and angular momentum eigenvalues, wavefunctions, degeneracy, selection rules, centrifugal distortion, form of spectra.
-
- Brown: 26-29
Bernath: 174-176, 185-200
Zare: 85-86, 89
Hollas: 103-105, 113-114
Banwell: 31-50
Levine: 195-213
- Geometry data and rotational constants of molecules
- Homework
- Problem 6: Pure rotational transitions of 12C32S in the ground vibrational state are observed in the microwaves at the frequencies 48990.978 MHz (J=0→1), 97980.950 MHz (J=1→2), 146969.033 MHz (J=2→3), 195954.226 MHz (J=3→4). Determine the the spectroscopic constants based on the transitions ovserved. Caclulate the bond length at the ground vibraional state.
- 22/11/2024: Vibrational spectroscopy of diatomic molecules: Potential energy curve, harmonic oscillator, Morse potential, energy, quantum numbers, energy levels, vibrational population distribution, zero point energy, spectroscopic constants, wave functions, selection rules, Dunham coefficients.
- Bernath: 208-221
Hollas: 137-147
Banwell: 55-63
McHale: 248-257, 266-267
Brown: 32-42
- Homework
- Problem 7: Calculate the force constant (in N/m) for H2 (ùe = 4320 cm-1) and Na2 (ùe = 0.221 cm-1).
- Problem 8: Write down the expression for the vibrational transitions with Äv = 1 of a diatomic molecule described by the spectroscopic constants ùe, ùexe, ùeye, Calculate the transition wavenumber for v" = 5 of NaBr for which these constants have the following values 315 cm-1, 1.15 cm-1 and 0.0008 cm-1.
- 29/11/2024: Vibrational spectroscopy of diatomic molecules: vibrational and rotational, coupling constants of vibrational and rotational motion, vibrational-rotational transitions, R and P branches, spectral patterns, mass dependence of Dunham coefficients on isotope substitution
- Bernath: 223
Hollas: 147-151
Levine: 142-174
Banwell: 63-71
Brown: 42-49
- Homework
- Problem 9: Write down the expression for the vibrational and rotational transitions belonging to the P branch of the first overtone transition of a diatomic molecule described by the spectroscopic constants ùe, ùexe, ùeye, Be, áe.
- 6/12/2024: Vibrational spectroscopy for polyatomic molecules: degrees of freedom, normal modes, local modes, types of vibrations (stretching, bending, etc.), degeneracy, vibrational angular momentum, types of potentials, rotational structure. Demonstration of normal modes on the computer using GausView. Fourier transform, interferometer and mathematical expressions.
- Bernath: 226-230, 248, 250, 256-259, 262-264, 268, 270-271, 280
Hollas: 154-162, 166-168, 174-195
Banwell: 71-83
McHale: 270-305
Levine: 235-245, 258-260
- Homework
- Problem 10: Make a rough drawing of the potential energy curve for the internal rotation of 1,2-dichloroethane and 2-fluoro-ethenol.
- Problem 11: H2O spectroscopic constants for its ground electronic state (íi is used in place of ùe): í1 = 3825.32 cm-1, í2 = 1653.91 cm-1, í3 = 3935.59 cm-1, x11 = -43.89 cm-1, x22 = -19.5 cm-1, x33 = -46.37 cm-1, x12 = -20.02 cm-1, x13 = -155.06 cm-1, x23 = -19.81 cm-1. Calculate the wavenumber for the following vibrational transitions: (v1" v2" v3") → (v1' v2' v3') = (000) → (001), (000) → (201), (000) → (004).
- 13/12/2024: Vibrational spectroscopy of polyatomic molecules: overtone and combination transitions. Electronic spectroscopy of diatomic molecules: Potential energy curves, quantum numbers, nomenclature, spectroscopic terms, selection rules. Shapes of spectra, positions and shapes of potential energy curves, line position calculation, Fortrat diagrams, Hund's cases of angular momentum coupling, sequences and progressions.
- Bernath: 24, 321-326
Hollas: 48-59, 225-237
Banwell: 20-26, 93-96, 162-163, 182-186
Brown: 57-60, 64-74
- Homework
- Problem 12: Indicate which of the following transitions are allowed and which are forbidden. i) 2Ð3/2 - 2Ö5/2, ii) 2Ð3/2 - 1Ó+, iii) 1Ðu - 3Ðg, iv) 2Ð3/2 - 2Ó-, v) 1Ó-g - 1Ó-g, vi) 1Ð3/2 - 1Ð3/2
- 20/12/2024: Electronic spectroscopy of polyatomic molecules. Demonstration of infrared spectrophotometers, standard (dispersive) and Fourier transform (with interferometer), Raman Fourier transform spectrometer. Lasers: features, types of materials, modes of operation.
- Bernath: 379-385, 388-390
Hollas: 260-261, 275-276, 278-381, 283-284, 337-342, 346-360
- Homework
- Problem 13:
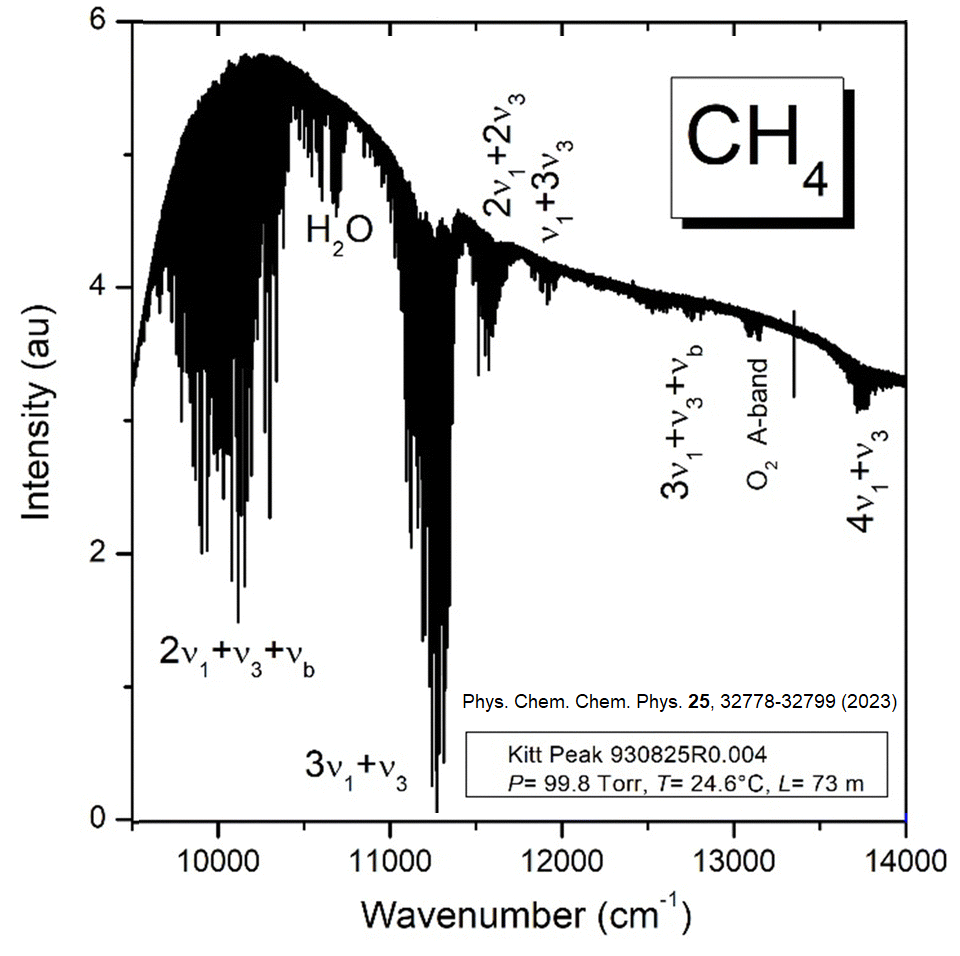 The adjacent spectrum was published in the paper "The high resolution absorption spectrum of methane in the 10800-14000 cm-1 region: literature review, new results and perspectives", A. Campargue, E. V. Karlovets, S. S. Vasilchenko and M. Turbet, Phys. Chem. Chem. Phys. 25, 32778-32799 (2023) [doi: 10.1039/d3cp02385k]. Calculate the spectroscopic constants í1, í3, íb using the average values of the bands shown.
The adjacent spectrum was published in the paper "The high resolution absorption spectrum of methane in the 10800-14000 cm-1 region: literature review, new results and perspectives", A. Campargue, E. V. Karlovets, S. S. Vasilchenko and M. Turbet, Phys. Chem. Chem. Phys. 25, 32778-32799 (2023) [doi: 10.1039/d3cp02385k]. Calculate the spectroscopic constants í1, í3, íb using the average values of the bands shown.
- 10/1/2025: Spectroscopic techniques: Auger, MPI, REMPI, CARS, CRDS. Spectroscopy applications in astronomy and study of reaction mechanisms.
-
Hollas: 371-374, 289-295, 315-322, 382-387
Brown: 78-84
Attard & Barnes: 43-47
Brouard: 33-34
Back to Molecular Spectroscopy course webpage
 The adjacent spectrum was published in the paper "The high resolution absorption spectrum of methane in the 10800-14000 cm-1 region: literature review, new results and perspectives", A. Campargue, E. V. Karlovets, S. S. Vasilchenko and M. Turbet, Phys. Chem. Chem. Phys. 25, 32778-32799 (2023) [doi: 10.1039/d3cp02385k]. Calculate the spectroscopic constants í1, í3, íb using the average values of the bands shown.
The adjacent spectrum was published in the paper "The high resolution absorption spectrum of methane in the 10800-14000 cm-1 region: literature review, new results and perspectives", A. Campargue, E. V. Karlovets, S. S. Vasilchenko and M. Turbet, Phys. Chem. Chem. Phys. 25, 32778-32799 (2023) [doi: 10.1039/d3cp02385k]. Calculate the spectroscopic constants í1, í3, íb using the average values of the bands shown.