Material taught, literature references, homework

7/10/2022: What is and what is not discussed as Spectroscopy. Quantities involved. Appearance of a spectum. Basic equations and spectral regions.

Hollas: xxi-xxv, 27-29, 41-43
Bernath (2nd Ed.): 3-7

14/10/2022: Blackbody radiation, Planck distribution, Einstein coefficients

Hollas: 27-39
Bernath: 7-11
McHale: 48-51
Softley: 1-6
Brown: 1-5, 15-17

Homework

Problem 1: A well-known laser, the Nd:YAG laser emits light at λ = 1064 nm. Calculate the frequency, the wavenumber (inverse wavelength), the energy per photon (in joules and eV) of this radiation and determine what spectral region in belongs to.

Problem 2: Using Wien's diplacement constant (found in the literature) determine the wavelength of maximum intensity of radiation emitted from a blackbody of temperature equal to that of a human body.

21/10/2022: Line shapes, broadening effects: Natural, Doppler, pressure, etc. Atomic spectroscopy: Hydrogen-like atoms.

Hollas: 34-39, 1-12
Bernath: 18-34, 109-111, 115-116
Softley: 29-30
McHale: 167-170, 175-176

Homework

Problem 3: The lifetime of the Ba ¹ P_1/2 - ¹S transition at 553.6 nm is 8.37 ±0.08 ns [S. Niggli, M. C. E. Huber, Phys. Rev. A 39 3924 (1989) PDF]. Calculate the Einstein coefficients A₂₁, B₂₁ and B₁₂ for this transition.

Problem 4: A ensemble of Ba atoms at 800 °C in the gas phase are excited in the ¹ P_1/2 - ¹S transition. What is the expected linewidth?

4/11/2021: Atomic Spectroscopy: Hydrogen-like atoms, wave functions, spin-orbit coupling, fine structure, hyperfine structure. Multielectron atoms: spectroscopic terms, Grotrian diagrams, qunatum defect theory, spin multiplicity, allowed and forbidden transitions

Hollas: 199-201, 213-222, 105-106
Bernath: 109-141
Sobelman: 5-15, 20-22, 34-38, 39-42
Herzberg Atomic Spectra: 20, 26, 50-61, 64-66, 71-78
Banwell: 139-148

Spectra of H, O, He, Ne, Ar, Na, Li, sun

Homework

Problem 5: Calculate the wavenumber and the wvelength of the second Pfund line for tritium and determine its fine structure.

Problem 6: From the paper Observation of the 1S-2S transition in trapped antihydrogen, M. Ahmadi et al., Nature 541 506-512 (2017) find the lifetime of the forbidden transition 1S - 2S for the hydrogen atom.

11/11/2022: Rotational spectroscopy: enery levels, angular momentum, moments of inertia of molecules, calculating moments of inertia, types of tops. Diatomic and linear molecules: hamiltonian operator, quantum numbers, energy eigenvalues, wave functions, degeneracy, selection rules, population distributions, peak positions, form of spectra, isotope effect.

Brown: 21-26
Hollas: 103-111
Bernath: 169-177
McHale: 209-212
Carrington: 146-152
Levine: 165-168

Homework

Problem 7: Using data from CRC Handbook of Chemistry and Physics (9- 15-41) caclulate the moments of inertia for the moelcules HCl, FCN (linear), SF₆ (octahedral) and the rotational spectroscopic constants (in cm^-1) for the first two. Use the masses of the most abundant isotopes.

18/11/2022: Rotational spectroscopy of non-linear molecules: Hamiltonian operator, quantum numbers, energy and angular momentum eigenvalues, wavefunctions, degeneracy, selection rules, centrifugal distortion, form of spectra.

Brown: 26-29
Bernath: 174-176, 185-200
Zare: 85-86, 89
Hollas: 103-105, 113-114
Banwell: 31-50
Levine: 195-213

Geometry data and rotational constants of molecules

Homework

Problem 8: Calculate line positions and approximate intensities of the rotational spectrum of gaseous ¹²C¹H³⁵Cl₃ at 20 °C. Given: B = 0.11015 cm^-1, C = 0.05932 cm^-1

25/11/2022: Vibrational spectroscopy of diatomic molecules: Potential energy curve, Morse potential, energy, quantum numbers, energy level, zero point energy, spectroscopic constants, wave functions, selection rules, peak positions, form of spectra, rotational structure of vibrational transitions, P and R branches, Dunham coefficients.

Bernath: 208-220, 223-224
Hollas: 116-119, 126-131, 137-151
Banwell: 51, 55-69

Homework

Problem 9: 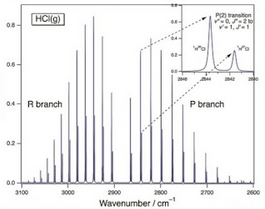Simulate the spectrum of the vibrational transition v = 0 → 1 with rotational structure of ¹H³⁵Cl at 300 K. The required spectroscopic constants are ω_e = 2990.946 cm^-1, ω_ex_e = 52.8186 cm^-1, B = 10.593 cm^-1, α_e = 0.30718 cm^-1.

2/12/2022: Vibrational spectroscopy of diatomic molecules: mass dependence of Dunham constants. Vibrational spectroscopy for polyatomic molecules: degrees of freedom, normal modes, local modes, types of vibrations (streching, bending, etc.), degeneracy, vibrational angular momentum, types of potentials, rotational structure. Demonstration of normal modes on the computer using GausView. Demonstration of infrared spectrophotometers, standard (dispersive) and Fourier transform (with interferometer).

Bernath: 226-230, 248, 250, 256-259, 262-264, 268, 270-271, 280
Hollas: 154-162, 166-168, 174-195
Banwell: 71-83
Levine: 235-245, 258-260

Homework

Problem 10: Fermi resonance occurs when two energy levels are very close. Consider the case of the vibrational states of CO₂ (v₁, v₂, v₃) = (1,0,0) and (v₁, v₂, v₃) = (0,2 (l₂=0),0). Vibrational and anharmonicity constants for ¹²C¹⁶O₂ are: ω₁ = 1354.07 cm^-1, ω₂ = 672.95 cm^-1, ω₃ = 2396.30 cm^-1 και x₁₁ = -3.10 cm^-1, x₂₂ = 1.59 cm^-1, x₃₃ = -12.50 cm^-1, x₁₂ = -5.37 cm^-1, x₁₃ = -19.27 cm^-1, x₂₃ = -12.51 cm^-1, g₂₂ = -0.62 cm^-1.

9/12/2022: Fourier transform, interferometer and mathematical epxressions. Vibrational spectroscopy of polyatomic molecules: overtone and combination transitions. Electronic spectroscopy of diatomic molecules: Potential energy curves, quantum numbers, nomencleture, spectroscopic terms, selection rules.

Bernath: 24, 321-326
Hollas: 48-59, 225-237
Banwell: 20-26, 93-96, 162-163, 182-186
Brown: 57-60, 64-67, 69-70

Homework

Problem 11: Indicate which of the following transitions are allowed and which are forbidden. i) ²Π_3/2 - ²Φ_5/2, ii) ²Π_3/2 - ¹Σ⁺, iii) ¹Π_u - ³Π_g, iv) ²Π_3/2 - ²Σ^-, v) ¹Σ^-_g - ¹Σ^-_g, vi) ¹Π_3/2 - ¹Π_3/2

16/12/2022: Electronic spectroscopy: shapes of spectra, positions and shapes of potential energy curves, line position calculation, Fortrat diagrams, Hund's cases of angular momentum coupling, sequences and progressions, iodine spectrum, C₂. Demonstration of gas flame and visible spectrophotometer.

Bernath: 326-337
Hollas: 240-250, 254-260
Gaydon, Spectroscopy of Flames
Gaydon, Flames. Their structure, radiation, and temperature

Homework

Problem 12: Draw the Fortrat diagram for the P and R branches of the transitions I₂ B ³Π_0u⁺ - X ¹Σ⁺_g (v',v")=(21,0) and (22,0) for J < 200. Use the following spectroscopic constants (in cm^-1): X ¹Σ⁺_g: T_e = 0, ω_e = 214.502, ω_ex_e = 0.61468, B_e = 0.0373719, α_e = 0.00011376, B ³Π_0u⁺: T_e = 15769, ω_e = 125.697, ω_ex_e = 0.7642, ω_ey_e = -0.00177598, B_e = 0.029039, α_e = 0.0001582.

>α_e = 0.0001582.

23/12/2022: Electronic spectroscopy of polyatomic molecules. The fate of an excited molecule: fluorescence, phosphorescence, ionization, dissociation. Spectroscopic techniques. Lasers: features, types of materials, modes of operation.

Bernath: 382-385, 388-391
Brown: 74-84
Hollas: 260-261, 278-280, 283-284, 289-295, 337-343, 346-362